AtCoder Begginer Contest 399に参加しました。
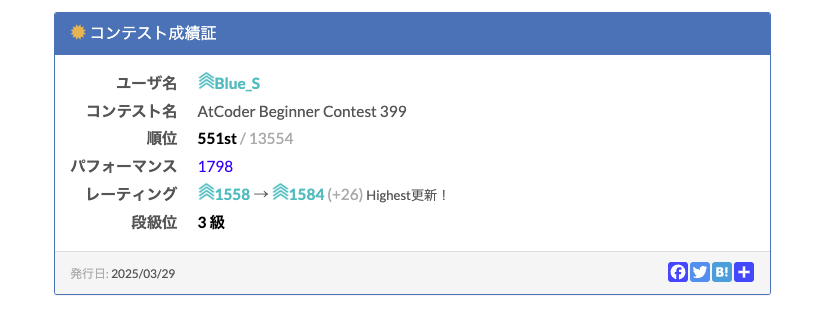
なんとまたまた青perfです。今回は青になることを目指していたので嬉しくはないのですが、青perf自体は喜んでもいいのでしょうか。入青は来週になりそうですね。
問題の解き方
A. Hamming Distance
これをハミング距離というんですね。愚直に実装するだけですが、本当に距離になっているのでしょうか。
任意の長さ \(N\) の文字列全体の集合を \(S\) とします。
\[\forall s, t \in S, d(s, t) = 0 \to s = t \\ \forall s, t \in S, d(s, t) = d(t, s) \\ \forall s, t, u \in S, d(s, t) + d(t, u) \ge d(s, u)\]
最後の式は、 \(s\) を直接 \(u\) に合わせに行くか、 \(t\) を経由するかで必ず後者が大きくなることがわかります。これは確かに距離ですね。
fn main() {
input! {
n: usize,
s: Bytes,
t: Bytes,
}
println!("{}", s.iter().zip(t.iter()).filter(|(s, t)| s != t).count());
}B. Ranking with Ties
ほとんどソートですが、いい感じにまとめないといけなくて大変ですね。 \(O(N^2)\) でも通ると書いてあるので、それでやりました。 \(P\) の値の上限が小さいのでカウントしてもできますね。
fn main() {
input! {
n: usize,
p: [usize; n],
}
let mut q = p.clone();
q.sort_unstable();
q.reverse();
for &p in &p {
println!("{}", q.iter().position(|q| *q == p).unwrap() + 1);
}
}C. Make it Forest
森にするためにはそれぞれの連結成分で木を作る必要があり、その状態がすでに森なので最適です。連結成分で木を作ることは必ずでき、木の辺は頂点数から \(1\) を引いたものなので、UnionFindで連結成分を管理すれば良いです。
fn main() {
input! {
n: usize,
m: usize,
uv: [(Usize1, Usize1); m],
}
let mut dsu = DisjointSetUnion::new(n);
for &(u, v) in &uv {
dsu.unite(u, v);
}
println!(
"{}",
m - (0..n)
.map(|i| if dsu.root(i) == i { dsu.size(i) - 1 } else { 0 })
.sum::<usize>()
);
}簡単ですね。350点なのはUnionFind, DFS, BFSのいずれかを必要とするからでしょうか。
ところで、UnionFindではなくDisjointSetUnionと呼ぶのが好きなんですよね。懐かしのLebesgue積分の香りがして良いです。
D. Switch Seats
問題文を見るとやるだけ(隣り合うところだけを確認すれば良いので \(O(N)\) であること)がすぐにわかります。が、実装方法をちゃんとしないとめんどくさい問題でした。
fn main() {
input! {
t: usize,
}
for _ in 0..t {
input! {
n: usize,
a: [Usize1; 2 * n],
}
let mut pos0 = vec![n; n];
let mut pos1 = vec![n; n];
for (i, &a) in a.iter().enumerate() {
if pos0[a] == n {
pos0[a] = i;
} else {
pos1[a] = i;
}
}
let mut b = vec![];
for (i, &a) in a.iter().enumerate() {
if pos0[a] == i {
b.push(pos1[a]);
} else {
b.push(pos0[a]);
}
}
let mut ans = 0usize;
for i in 0..2 * n - 1 {
let x = a[i];
let y = a[i + 1];
if x == y {
continue;
}
let k = b[i];
let l = b[i + 1];
if i.abs_diff(k) != 1 && (i + 1).abs_diff(l) != 1 && k.abs_diff(l) == 1 {
ans += 1;
}
}
println!("{}", ans / 2);
}
}コード長が長いですね。こういうのを綺麗なコードで書きたい。
最初、確認をカップル番号順にやろうとして2ペナしました。考察は正しくても実装方針(何を順番に見ていくか)を間違えるとペナが出やすい問題で、教育的ですね。
コードの解説ですが、 \(b_i\) は \(a_i\) の相方が座っているインデックスです。
E. Replace
まとめていくだけなので、UnionFindで何とかして、、、とやっていました。このような有向関係はちゃんとグラフ作った方が良いんですね。楽をしようとしてとんでもない実装になり、頭が爆発しました。どっちみち、三角ループに一つついた形もペナルティがつくと思っていたので考察ミスでした。
大体の方針はわかっていたので、ちゃんと紙に書いて整理しながらやるべきだったかもしれません。このような問題に喰らいつけるようになったのは成長かなと思います。あとは、典型的な実装方法を学ぶだけ??
F. Range Power Sum
式変形をする問題です。このような \(A\) の区間和は、累積和に一旦直すと見やすくなります。それに加えて \(l, r\) も分解します。このような複雑な区間を考えるのは難しいのですよね。 \(f(l, r) = f(r, l)\) が成り立つ問題であれば全体を求めて斜めを引いて2で割るが有効ですが、今回はそういう問題ではないので、見やすくするために総和を分解してしまうのが好きです。
\[\sum_{r=0}^N \sum_{l=0}^{r-1} (S_r – S_l)^K = \sum_{i=0}^K {}_K C_i (-1)^i \sum_{r=0}^N S_r^{K-i} \sum_{l=0}^{r-1} S_l^i\]
です。これは、 \(S_l^i\) の累積和をとりながら、二つ目の総和を計算できます。計算量は、 O(NK \log K) です。
fn main() {
input! {
n: usize,
k: usize,
a: [u64; n],
}
let mut fact = vec![GF::<MOD>::new(1)];
for i in 1..=100 {
fact.push(fact.last().unwrap() * gf!(i));
}
let mut s = vec![GF::<MOD>::new(0)];
for &a in &a {
s.push(s.last().unwrap() + gf!(a));
}
let mut ans = GF::<MOD>::new(0);
for i in 0..=k {
let mut res = GF::<MOD>::new(0);
let mut tmp = GF::<MOD>::new(0);
for r in 0..=n {
res += s[r].pow((k - i) as u64) * tmp;
tmp += s[r].pow(i as u64);
}
ans += fact[k] / fact[i] / fact[k - i] * if i % 2 == 0 { gf!(1) } else { gf!(-1) } * res;
}
println!("{}", ans);
}知らない解説がたくさんありました。積の和is何なので、ちゃんと復習したいですね。形を見た感じ、FPS感もありました。解説にもあったのでそれも読んでおきたいです。
感想
1問解けない問題が途中にあると負けた感じがします。全くわからない問題がなくなってきていて、解法は大体わかるのに、、、みたいな回が増えている気がします。いい傾向な気がします。
大胆予想(嘘注意)
400と言えば閏年の例外ですね。4年に一度の閏年ですが、実は400の倍数で調整のために閏年がなくなっています。次回は閏年に関連した曜日の問題が出ると予想して、関数を作っています。AのFAはいただきます。対戦よろしくお願いします。
これはCTAサンプルです。
内容を編集するか削除してください。



